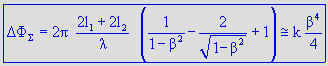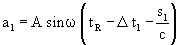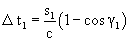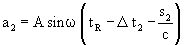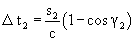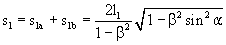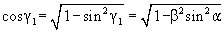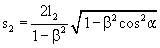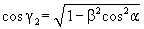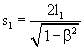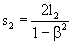The Michelson-Morley Experiment:

AN IMPROVED METHOD OF CALCULATING PHASE SHIFT
ARISING IN THE MOVING INTERFEROMETER

© Ferenc Kiefner, 2005

This is an HTML page from location http://www.kiefner.hu/view/mmximp.htm
You can also download this paper in PDF format
Comments are welcomed:

Copyright Notice / Terms of Use
The paper presented here is the intellectual property of the author. You may use it for any non-profit purpose as long as the contribution of the author is explicitly acknowledged.

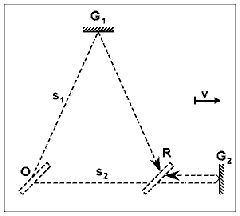
By means of the Michelson interferometer a number of experiments were carried out to demonstrate the translational motion of the earth. The author re-analyzes the method of calculation in these experiments, and shows that, when taking into account a factor so far judged negligible, the expectable total phase shift will be proportional to the fourth power of v/c (the ratio of translation speed to light velocity).
No hypothesis relating to the existence of a physical phenomenon or law unknown to date is cited in this article.

1. Introduction

More than a century has elapsed since 1887 when A. A. MICHELSON and E. W. MORLEY conducted their famous experiment [1], which was expected to reveal the translational motion of the earth. Although this experiment was repeated many times in the course of the years with the use of increasingly more sensitive equipment, no success could be attained in a reliable demonstration of the translational motion of earth. In addition to the experiments carried out with the use of the Michelson interferometer, experiments based on other methods have been conducted for the detection of this motion, but each of these also had a negative result or at least, a disputed one.

All these facts, however, do not exclude the possibility of making another analysis of the mentioned experiments on the basis of appropriate considerations. Of these, the author has selected the Michelson-Morley experiment as that to which a great conclusive force can be attributed, and, he now suggests an improved method of calculation.

Although the differences existing between the traditional and improved methods of calculation will be pointed out in several places, this article is not intended to give a comprehensive critique of the traditional method. The author's purpose is merely to draft a possible theoretical structure for calculation of arising phase shift.

It should be mentioned in advance that no hypothesis relating to the existence of a physical phenomenon or law unknown to date will be cited in this article.
We would like to emphasize that in our reasoning we shall adhere to the cornerstone of the traditional method of discussion, according to which light can be interpreted as a "classic" particle/wave phenomenon; i.e. light is a stream of corpuscles (photons) and at the same time it constitutes harmonic oscillations of electromagnetic field, therefore it propagates as a ray and also as a sine wave.
For this reason, the microstructure of light will not dealt with, and no quantum-optical considerations will be made in the calculation of the characteristics of interference. It is furthermore assumed that the characteristics of the experimental equipment and conditions have been idealized. Thus, for example, it is considered that light emitted from a source has a narrow spectrum and a large coherence length, etc.
In accordance with the traditional method of calculation the light diverging axial-symmetrically from the axes (arms) of the interferometer will not be drawn into the discussion; that is, the improved method of calculation will be applied only to the rays that are propagating strictly along the axes of the interferometer. In the figures also only these rays will be indicated.

As the Michelson-Morley experiment is well known, the related path calculation method will be described only in a concise summary in the Appendix, and the formulae and figure reported there will be referred to with the letter A preceding their reference numbers.

A scheme of the Michelson interferometer is shown in Fig. 1 in a position in which one of the arms - let this be K₂ - is parallel to the direction of motion.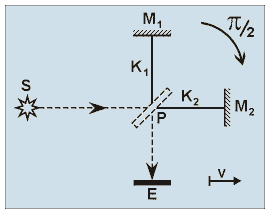

Figure 1. Scheme of the Michelson interferometer.

      

S ‑‑ light source; E ‑‑ screen for displaying the inter­ference pattern; K₁, K₂ ‑‑ perpendicular arms of the inter­ferometer; M₁, M₂ ‑‑ mirrors mounted on the ends of the arms; P ‑‑ semi-transparent mirror for splitting and recom­bining the light source's beam; v ‑‑ velocity vector of the translation.

When the interferometer used in the experiment is rotated through angle π/2, and one of the arms is parallel to the direction of motion in the initial and final positions (hereafter called main positions), according to traditional method the value of total phase shift arising between the rays travelling along the arms can be expressed in radians as follows:

.

For the sake of historical completness, it may be mentioned that in 1881, when Michelson and Morley first attempted to demonstrate the earth's translational motion in an experiment, they used twice larger value for awaited total phase shift

,

since the path of light perpendicular to the direction of motion was mis-modelled. On the basis of M. A. POTIER's comment, that error was corrected [3] in paper [1].

According to the improved method of calculation suggested by the author, the total phase shift will be calculable with the use of the formula

,

(1)

that is, the arising overall fringe shift in interference pattern will be proportional to fourth order effect in v/c.

In the following, we shall discuss how the formula (1) can be derived.

2. Inaccuracy implied in the traditional method of calculation

The progression of the interfering rays in the moving interferometer is shown in Fig. 2. The paths of rays are depicted in accordance with the traditional model. Those rays that propagate along the arms here are illustrated and only the positions of mirrors M₁, M₂ and the semi-transparent mirror P are indicated.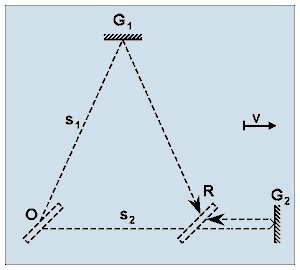

Figure 2. A model of light paths employed in the traditional method of calculation. According to this model, in the interferometer moving with translational speed v the light rays starting from the same position in the space will return to a common point.

      

O ‑‑ position of semi-transparent mirror P at the start of the light rays; R ‑‑ common return point of rays (position of mirror P on the return of the rays); s₁, s₂ ‑‑ paths of light rays along arms K₁, K₂, respectively; G₁, G₂ ‑‑ positions of mirrors M₁ and M₂ mounted on the ends of the arms upon the reflection of the light rays.

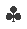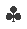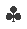
For the paths traversed, the following relationships can be written on the basis of formulae (A‑5) and (A‑6):

,

.

Thus, the sine waves of light arriving at point R from point O at moment t_R are described by the following equations:

,

,

	a1, a2	--	instantaneous amplitude of light rays travelling along arms K1 and K2 respectively in point R and at moment tR,
	A	--	amplitude of light wave,
	ω	--	cyclic frequency,
		--	phase of the ray of arm K1 in point R and at moment tR,
		--	phase of the ray of arm K2 in point R and at moment tR.

The rays emerge from a common light source, and for this reason the initial phases of the oscillations in the equations of the rays are identical. For the sake of simplicity, the initial phases have been taken for zero in the equations of the rays. This simplification will be employed later as well.

Subsequently, in addition to the commonly used concept of the initial phase the term "start phase of the ray" will be introduced as an auxiliary concept. For this reason it is considered very important that even now a clear discrimination should be made between the two concepts.
The term initial phase is used to denote the phase occurring at the spatial origin of the wave at moment t = 0. According to previous convention, this initial phase will be assumed as having a zero value.
The term start phase of the ray is used to denote the phase occurring at the spatial origin of the wave at an arbitrary moment t, and thus the notion of start phase appears in this paper as a generalization of the concept "initial phase". According to this, at the moment t = 0 the start phase value of the wave will be equal to the initial phase value, while at other moments it differs from that by ωt. Thus, the start phase can be regarded as a function of time.

In Fig. 2, the ray progressions shown in the model tacitly assume that the light rays starting from an the same (point O) of the moving mirror P and travelling strictly along the arms will return to a common location (point R).

Let us now show that this assumption in the model, as shown in Fig. 2, generally leads to an inaccuracy.
The light ray advancing along arm K₁ at speed c covers the path s₁ during a time t₁. During this time interval mirror P travelling at velocity v traverses a path

.

Likewise, the light ray advancing along arm K₂ at velocity c covers path s₂ during a time t₂. In this time interval, mirror P moving at velocity v covers a path of

.

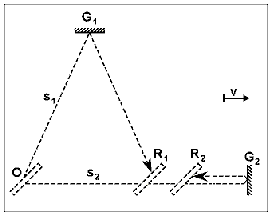
Taking this fact into consideration, the accurate ray path of the traditional model can generally be illustrated as shown in Fig. 3.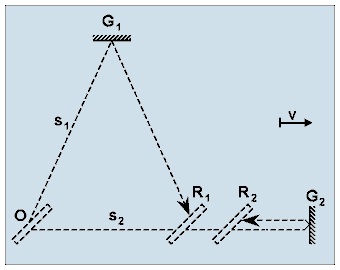

Figure 3. Analysis of the velocity and path conditions reveals that generally the return point of light rays starting from the same location can be different. This fact has already been pointed out by Michelson and Morley, but they decided its effect negligible.

      

R₁ ‑‑ return point of the ray of arm K₁ to mir­ror P; R₂ ‑‑ return point of the ray of arm K₂ to mirror P; others ‑‑ see above.

According to the earlier analysis, the lengths of sections OR₁ and OR₂ are:

,

.

According to the earlier analysis, the lengths of sections OR₁ and OR₂ are:

,

.

In a given position of the interferometer the length of these two sections could be equal only when a relationship of

exists between the lengths of the arms. However, upon rotation of the interferometer, the equality of sections OR₁ and OR₂ ceases to exist even in the case of the existence of the aforementioned relationship. According to this, since the two sections are not generally equal, point R splits into points R₁ and R₂.

The question detailed above was also mentioned [2] in article [1]. However, in the absence of any detailed numerical assessment thereof, its effect was considered negligible.

The relevant literature seems to be uniform in discussing the principles of method of calculation applied with the Michelson interferometer. It ignores the apparent possibility of inaccuracy, or rather, it does not even make mention of it. For this reason, the references are limited to article [1], since it has already revealed the possible source of inaccuracy.

The problem becomes particularly acute, if the lengths of the arms (l₁, l₂) differ greatly from each other. Then, the lengths of light paths (s₁, s₂) may also be considerably dissimilar with each other. Consequently, the distance

existing between the returning light rays could also be increased significantly. In such a case, if a point-like test object were placed between the light source and mirror P, a doubling of the image of the test object, in compliance with the traditional model, would become possible upon sufficient change in translation velocity.

To summarize, it seems to be expedient to make a proposal for a model that excludes the previously revealed possibility of inaccuracy, or one that can be employed in the case of an arbitrary arm length and velocity.

3. The proposed model and method of calculation

Accurately retaining the path length of the rays (s₁, s₂), we must correct the traditional model so that the above mentioned possibility of inaccuracy will not occur in the modified model. The proposed model, shown below in Fig. 4, attempts to fulfill these requirements.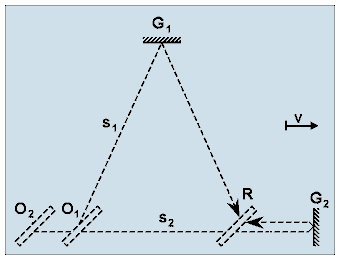

Figure 4. Model of the light paths applied to the improved method of calculation. The corrected model permits rays returning to a common point to start from different points in space. At the same time this also implies that the start phases of the two light rays can differ from each other. The possibility of inaccu­racy inherent in the traditional method can be eliminated by using this model.

      

R ‑‑ common return point of rays at mirror P; O₁ ‑‑ starting point of a ray of arm K₁ from mir­ror P; O₂ ‑‑ starting point of a ray of arm K₂ from mirror P; others ‑‑ see above.

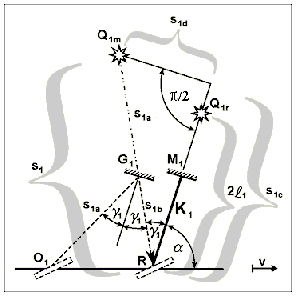
While in the traditional model (shown in Fig. 3) the rays propagating strictly along the axes started from the same point O but arrived at different spatial points R₁ and R₂, these rays return to the same point R in the proposed corrected model. As a consequence of this, the previously mentioned possibility of inaccuracy cannot occur regardless of the length of the arms or the speed of the translational motion.

In the revisited model, however, it has to be taken into account that the rays returning to point R may start from different positions of the moving mirror P (points O₁ and O₂) and, consequently, at different moments in time. Therefore, the start phase of these rays can differ by some ωΔt, where Δt is the difference between the starting times of the rays outgoing from points O₁ and O₂.

Thus, not only is the change in spatial conditions (path lengths) taken into account among the consequences of motion, but the traditional method of calculation is enhanced by regarding the altered time conditions (start phases) as well.

The same evident procedure employed by the traditional method will be used to calculate the path lengths of the light rays. The method of calculation in this article will be improved only by determining the difference of start phases ωΔt of the light rays outgoing from points O₁ and O₂. Here, ω is constant and known and thus the unknown Δt has to be calculated.

In the course of the calculations it should be naturally requested that in the case of v → 0 each of the formulae should be transformed into generally accepted formulae or should adopt those values, that this formulae give for resting interferometers. The reader can check the fulfillment of this requirement later.

The interferometer will be broken down into two subsystems, one each for arms K₁ and K₂, for the calculations. The quantities of the individual subsystems will, as previously, be distinguished by subscripts 1 and 2. To unite the two subsystems the time moment t_R, when the arms just pass through the point R, was chosen as the common reference point for the time-counting.

In what follows, the path of a ray in one of the subsystems, let this be the arm K₁ subsystem, will be studied in detail. To this end, a ray that travels along the appropriate axis in an arbitrary position of the interferometer, will be plotted on the basis of Fig. A-1. In this position the arm K₁ subtends angle α with the direction of motion, and the characteristics of light ray can readily be examined.
The path length s₁ and deflection angle γ₁ of the path of the ray shown in the figure are yielded by the calculations contained in the Appendix (as a function of quantities l₁, α and β).

To facilitate the analysis, the light source is assumed to be located directly at mirror P which is rigidly connected with the arms. Fig. 5 shows the equivalent image of the light source, which can be observed at point R. This image is considered a virtual light source.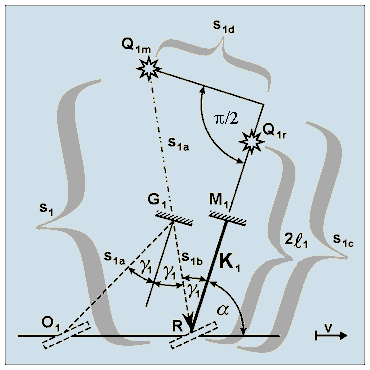

Figure 5. Path of a light ray travelling along arm K₁ of the interferometer in case of an arbitrary angle α. In order to achieve a surveyable illustration and facilitate the calculations, the path of a ray is shown as outgoing from the virtual light source, which can be observed at point R. With the interfero­meter at rest, a light ray would travel a path of 2l₁ in length along the arm. When the interfero­meter is moving, the path of light becomes elongated (s₁ > 2l₁), and it sub­tends angle γ₁ with the arm.

      

Q_1r ‑‑ virtual light source visible from point R with the interferometer at rest; Q_1m ‑‑ virtual light source visible from point R with the interferometer in motion; γ₁ ‑‑ angle subtended by the light ray with arm K₁; s_1a, s_1b ‑‑ portions of the path of a light ray from point O₁ to point G₁ and from point G₁ to point R, respectively; s_1c, s_1d ‑‑ components of the path of light ray s₁ parallel and perpendicular respectively to arm K₁; others ‑‑ see above.

We shall investigate the position of the virtual light source in two different states of motion. In the figure Q_1r denotes the position of virtual light source in a resting interferometer (v = 0), while Q_1m marks the position of virtual light source in a moving interferometer (v > 0). For a better demonstration of the spatial positions Q_1r and Q_1m of virtual light source, a prolonged line is drawn along arm K₁ with a short break in continuity.

With the interferometer at rest, the virtual light source would constantly be located in point Q_1r on the prolonged line of arm K₁, i.e. at moment t_R it can also be found there. At this time the light ray starting from point Q_1r could be described in point R and at moment t_R by the equation

.

When the interferometer is moving at speed v, the light ray in point R and at moment t_R is not represented correctly by the above equation because

To sum up, it may be stated that the path of the light ray not only lengthened (s₁ > 2l₁) but also "turned back" from arm K₁ around point R (γ₁ > 0), and, thus, the light source Q_1m has arrived behind the prolonged line of arm K₁.
As we previously assumed, the light source is located at mirror P which is rigidly connected with the arms, and, the arms pass through point R at moment t_R. Therefore, the virtual light source had to cross point Q_1m in the process of motion at a moment prior to t_R. This moment is denoted by t_R - Δt₁, where Δt₁ is a still unknown time interval.
Consequently, the start phase of the light ray outgoing from point Q_1m is not ωt_R but something smaller by an ωΔt₁ value.

According to the above reasoning, in the case of a moving interferometer the light ray is described correctly in point R and at moment t_R by the equation

.

This formula reflects the fact that in point R the phase of the ray is affected by the lengthened path (Δl₁) as well as the changed start phase (ωΔt₁) on account of the light ray's deflection.
Hence, the total length of the light's path will be

.

.

(2)

When the value of component s_1d is zero, i.e. when the virtual source is located on the line of arm K₁, the value Δt₁ obviously will also be zero. (This also holds true when simultaneously s_1c > 2l₁, which is possible if α = 0 and v > 0.) On the basis of this, it can be stated that the appearance of the time interval Δt₁ is due to the spatial distance s_1d arising between the virtual light source Q_1m and the line of arm K₁.

.

Should the light travel along s_1c, time interval t_1c would require:

.

An unknown supplementary interval Δt₁ must be added to time interval t_1c to obtain time interval t₁, during which the light ray can cover path s₁. Thus, with interval Δt₁ added, the component s_1d, which is perpendicular to the arm, is created in addition to the component s_1c coinciding with the direction of the arm:

.

According to the geometry of Fig. 5, the length of s_1c is

.

With t₁, t_1c and s_1c eliminated, the unknown Δt₁ can be obtained from the above set of four equations as a function of quantities s₁ and γ₁.
Solving the set of equations will yield

.

(3)

.

Notably, in the case of α = 0 (arm K₁ is parallel to the direction of motion) Δt₁ will assume a zero value at any velocity, since the light ray does not deflect laterally from the arm.

An entirely analogous procedure can be adopted in investigation of a ray travelling in the arm K₂ subsystem. Thus,

,

(4)

.

(5)

,

in the formulae (2) and (4), where Φ₁ and Φ₂ are the phases of light rays returning to point R at moment t_R.
Let us determine the phase shift ΔΦ of the two incident rays for an arbitrary angle α.

,

where Δt₁ ‑ Δt₂ = Δt gives the difference between the starting times of the rays outgoing from points O₁ and O₂.

Let us calculate the total phase shift ΔΦ_Σ for main positions, when arm K₁ was at a right angle to the direction of motion (α = π/2) before the interferometer was rotated through angle π/2. Then

.

By substituting here the values of s₁ and s₂ from expressions (A-1) and (A-3), Δt₁ and Δt₂ from expressions (3) and (5), cos  γ₁ and cos γ₂ from expressions (A-2) and (A-4), and by using relationship

,

.

(6)

Assuming that β << 1, let us expand the expressions and into a series, omitting the higher-order members from β⁶ onward. Then the following expression will be obtained:

.

(7)

By using (7) and the earlier introduced notation k = 2π(2l₁+2l₂)/λ, formula (6), which supplies the value of the total phase shift ΔΦ_Σ, may be written as follows:

.

Thus, formula (1), which was presented earlier in this paper, has been completely deduced.

APPENDIX
Path calculation of the light rays

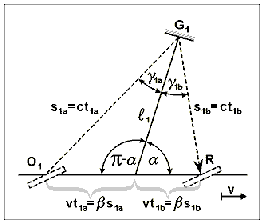
Let us examine the paths of rays that travel strictly along the arms, with the interferometer in an arbitrary position, when arm K₁ subtends angle α with the direction of motion. The interferometer is moving at the rate of speed of v, and the arms K₁ and K₂ have a length of l₁ and l₂, respectively.

The path of a ray of arm K₁ is indicated in Fig. A-1. For simplification of the formulae, let us stipulate that 0 ≤ α ≤ π/2.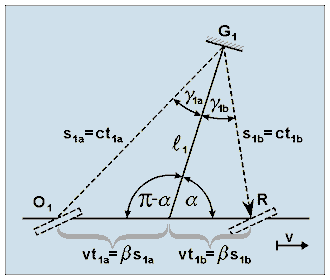

Figure A-1. The path of a ray of arm K₁ in the interferometer moving with translational speed v. Arm K₁ with length l₁ subtends an arbitrary angle α with the direction of motion.

      

O₁ ‑‑ position of semi-transparent mirror P at the start of the light ray; R ‑‑ return point of light ray to mirror P; G₁ ‑‑ position of mirror M₁ mounted on the end of arm upon the reflection of the light ray; s_1a, s_1b ‑‑ portions of the path of a light ray from point O₁ to point G₁ and from point G₁ to point R, respectively; γ_1a, γ_1b ‑‑ angles subtended by a light ray with arm; t_1a ‑‑ time interval in which the ray of light arrives at point G₁ from point O₁; t_1b ‑‑ time interval in which the light ray arrives at point R from point G₁.

Let us determine the quantities s_1a, s_1b, γ_1a and γ_1b (giving the path lengths and inclination angles of the ray) as the functions of quantities l₁, α and β.

Determination of the quantities sought is a simple geometric task; however, for the sake of completeness, the calculations are given below.

With reference to the figure, on the basis of the cosine law, it may be written that

,

.

.

(A-1)

,

.

,

,

and, in what follows, γ₁ will be written instead of γ_1a and γ_1b. Hence,

.

(A-2)

The path of a ray can be calculated in a perfectly analogous way for arm K₂. The only difference is that arm K₂ subtends angle α - π/2, not α, with the direction of motion. Accordingly,

	,	(A-3)
	.	(A-4)

By substitution α = π/2 into (A-1) and (A-3), the length of the paths will be obtained for the interferometer in the position shown in Fig. 1:

	,	(A-5)
	.	(A-6)

References

Symbols used in the paper

Symbols beginning with Roman characters:

Symbols beginning with Greek characters:

Original text: 1988

Last updated: August 19th, 2023